LAB - Buoyancy

We know specifically what the buoyant force is: the buoyant force on a submerged body must be equal to the weight of the fluid displaced by the submerged body. We can use this property of the buoyant force to measure the density of an object by submerging it in a fluid.

Density is mass over volume:    r = m/V.

Finding the density of an object can help us to identify the object because no matter what shape it is, or what it looks like, a given material has a constant density. We would like you to validate this procedure on a specimen of known density, and then identify an unknown object by calculating its density. You should measure the density of each, and then look on a table of densities to see if you can identify what the material is.

Archimedes’ principle states that a body immersed in a fluid experiences an upward force due to the surrounding fluid and that this force is equal to the weight of the fluid displaced by the body. We can make use of this principle to determine the volume or the density of various substances.

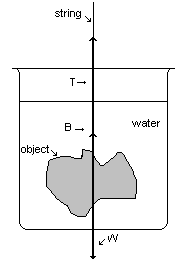
Consider a body immersed in water, as shown above. The density of the body is greater than that of water, and so to keep the object from sinking, we support it with a string. The tension T in the string plus the buoyant force B of the surrounding water is just sufficient to balance the weight W of the object.

That is,

W = T + B. (1)

We can use this equation to find the buoyant force by weighing the body in water to find T, provided we suspend the body from the weighing scales using the string. If we measure the weight out of the water and then the weight in the water, we can determine the buoyant force from this equation. (Apply equation 1 to the two different situations - out of the water, the buoyant force is zero.)

The buoyant force is the weight of the displaced water. The volume of displaced water is, of course, the same as that of the body. Since the buoyant force is the weight of the water displaced by the object, then the buoyant force is the density of the water multiplied by the volume multiplied by g:

. (2)

By definition, the density of water is exactly 1000 kg/m³, so using this equation, we can find the volume of the body using the buoyant force determined as in equation 1. If we know the volume and the real weight W, then we can determine the density of the object

. (3)

Apparatus

Spring scale
String
Container with water
One aluminum block/cylinder (alas, not everyone may actually have an aluminum block, it may just be another unknown one)
One unknown cube

 
In this picture, from left to right, if you have aluminum, it will be one of the two on the left. From left to right, alumunim cylinder, aluminum block, "unknown 1", "unknown 2", and "unknown 3". Unknowns may also come in cylindrical shape.
For your instructor, either identify them with the labels given above if you think you can translate the picture to what you have, or take a picture of your blocks and send them with your results to the instructor.

Procedure and Analysis:

1. Choose the known, aluminum block, first. Then do the unknown cube. For each of the objects, hold the spring scale and suspend the mass from it to read the weight.
2. Then submerge the mass in the container of water while still holding the scale with it suspended underneath. Take a new reading from the scale. 
3. You will end up with two readings for each object, one in the air and one in the water. These two readings allow you to determine the buoyant force on the object (see theory section if you do not know how.)
4. Determine the density for the known material and compare your calculated value to its listed density (see menu at left).  Be sure that your calculated density is close to the listed density to validate your procedure.
5. Now, using the density you calculated for the unknown object, determine the material it is made of by comparing your density to a chart of densities. It is fair to use additional observations other than simply density.
6. If this is a formal lab: For ONE of your measurements, estimate your precision from the precision of your scale readings (see below). 

Error Analysis:

Notice that if we solve equations 2 and 3 together, we get

recall that mg is the weight of the object, W. The error in the density is going to be due to the error in W and the error in B (each due to the imprecision of the scale, which you are going to have to estimate.)

For algebra-based physics (for calc-based, skip forward): recall that the error in density due to the error in weight is

,

and the error due to the error in the buoyant force is

.

For calc-based physics, you need to find the error in density due to the error in W and the error in density due to the error in B using partial derivatives.

You need to find the error in the density due to W, and the error due to B, and find the square-root of the sum of the squares (as we have done in the past with error propagation.)

Extra Credit: 

1. Does the real world aspect that the string has weight introduce an error into our estimation of the density?  Please back up your answer with an equation to show why you believe as you do.

2. Is the Energizer Bunny male or female?

Write-Up

1. If this is a formal lab (as indicated on the lab syllabus), you have been instructed as to whether this is an individual or group write-up, or an oral presentation. If it is a write-up, each person must submit the lab electronically as a word-processed document in Moodle before the next lab meeting. If it is a group write-up, you should all be submitting the same document. For written formal labs, remember to check the "write-up hints" page to be sure everything is included and check your write-up against the grading rubric.
2. If this is an informal lab, work on the results together in your groups, and be sure to have your complete informal lab in your lab notebook and checked by the instructor before you leave.
3. Remember to read the next lab and do the pre-lab before you come to lab next week! You may work on the pre-lab with others, but each person must submit her or his own work.

Department of Physics