Angular Acceleration and Moment of Inertia

I. Introduction

If we have a system which consists of a number (i) of masses, each with mass m_i with a distance from the axis of rotation, r_i, the moment of inertia of the system is defined as

. (1)

In words, multiply each mass by the square of its distance from the axis of rotation and sum all of these factors. Thus we may calculate the moment of inertia of a collection of objects. This is not always easy or even possible to do.

Alternatively, we can measure the moment of inertia of an object (or a system of masses) by measuring the angular acceleration a that results from a given applied torque t. The rotational analog of Newton’s second law of motion then gives

. (2)

In this lab you will experimentally measure the moment of inertia of an object by measuring the quantities in Equation 2. You will use the same apparatus you used to measure centripetal force, except that the mass and spring have been removed and the crossarm has been replaced by a threaded rod. Four wing nuts on the threaded rod are used to clamp two masses near its ends. The threaded rod and its attached masses are set into rotation by wrapping a string around the vertical post, running the string over the pulley, attaching the string to a weight hanger and allowing the weight hanger to fall.

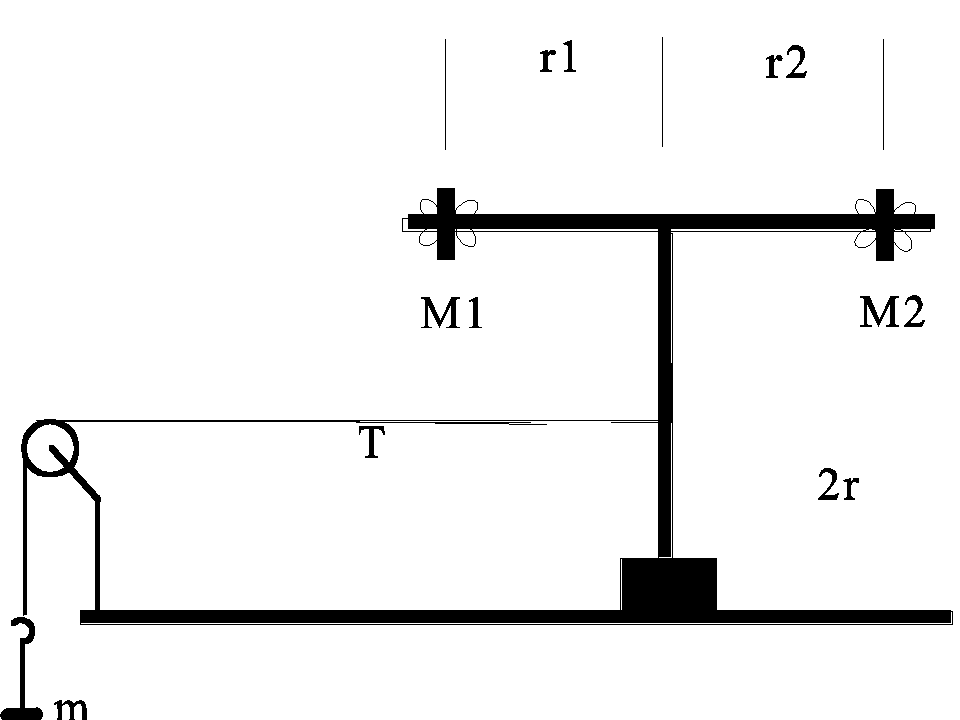
The constant tension in the string applied tangent to the vertical shaft gives rise to a constant torque and consequently to a constant angular acceleration.

In this lab, you will be asked to determine an appropriate procedure to measure the moment of inertia of the system, and to apply that procedure.