 |
|
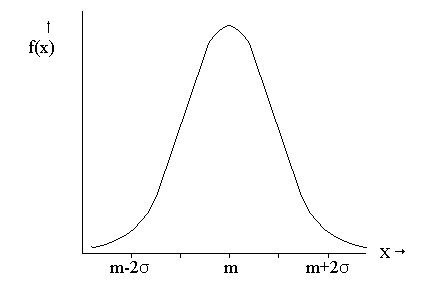
f(x) is the frequency of occurrence of x (a measured value) |
In the laboratory neither the measuring instrument nor the measuring procedure is ever perfect; consequently, every experiment is subject to experimental error. We needA reported result which does not include the experimental error is seriously incomplete.
Experimental errors are generally classified under two broad categories - systematic errors and random errors.
Systematic errors include errors due to the calibration of instruments and errors due to faulty procedures. When reporting results in scientific journals, one must often take great pains to assure that one's meter sticks and clocks, for example, have been accurately calibrated against international standards of length and time. However, even if an instrument has been properly calibrated, it can still be used in a fashion which leads to systematically wrong results.
Random errors include errors of judgment in reading a meter or a scale and errors due to fluctuating experimental conditions. In addition to environmental fluctuations (e.g., the temperature of the laboratory or the value of the line voltage), there will be fluctuations caused by the fact that many experimental parameters are not exactly defined. For example, the width of a table top might be said to be 1 meter, but close examination would show that opposite edges are not precisely parallel and a microscopic examination would reveal that the edges are quite rough. How, then, can we even define what we mean by the width of the table?
When the systematic errors in an experiment are small, the experiment is said to be accurate.
When the random errors in an experiment are small, the experiment is said to be precise.
Systematic errors are avoidable, and any time you determine that there is one, you should do your best to eliminate it. Random errors, on the other hand, are reducible in easy ways (using more precise measuring instruments), but are unavoidable. The sensitivity of your measuring instrument determines the ultimate precision of any measurement. Since random errors are unavoidable, we should never use a measuring instrument so crude that these random errors go undetected. We should always use a measuring instrument which is sufficiently sensitive so that duplicate measurements do not yield duplicate results. Correct procedure requires that you report your readings of scales and meters by estimating to one tenth of the smallest scale division (excluding, of course, those cases in which the instrument is designed to give digital readout).
| Concept check: If you flip a coin 10 times, how many times do you expect it to turn up heads? When you actually do this experiment, you do not find you get the expected answer every time. Is this due to random fluctuations or due to systematic error? Can you explain a situation where it would be due to both? I put the answer below so that you can try to figure it out on your own. |
Given the pervasiveness of random error, one of the tasks of the experimentalist is to estimate the probability that someone who performs an apparently identical experiment will obtain a different result (measuring the width of the table top mentioned above would be a simple example because, among other things, "width" can't be defined precisely). Subsequent measurements will not be expected to give the same answer, but multiple measurements will be distributed in such a way that we can make a good estimate of the "right" answer. If we made a lot of measurements of one quantity, and the error was truly random, we would expect to make as many measurements that are higher than the "correct" value as measurements that are lower. And we would expect to get fewer measurements that are further away from the "correct" value. If we were to plot the frequency of measurements vs. the value of the measurement, we most often expect to get a distribution that looks like the following:
 |
|
f(x) is the frequency of occurrence of x (a measured value) |
| Concept Check: As you are reading this, if you are having trouble picturing what we are talking about, think about flipping 10 coins all at once. How many heads do you get? You might get 6, you might get 4, you might get 1... or anything between 0 and 10. But you should expect to get 6 as many times as 4, and more times than 1, so if you plot the number of times you get each possible value, your distribution will look like this graph, with the middle, or mean value, being 5 (the value you should get most frequently). |
This distribution occurs so frequently for measurement that it is given two names: the Gaussian or the Normal distribution. Remember, we are talking about making multiple measurements of one quantity here - x is simply the value of the measurement we make (e.g. the width of the table) and f(x) is the number of times we come up with a particular number. The distribution of answers usually will look like this Normal distribution no matter what we are measuring, as long as we make a large number of measurements (note that if we take 2 or 3 measurements, there is no way we could get a distribution of measurements that looks this way). Statistical theory (beyond this class) allows us to determine an equation describing this curve:
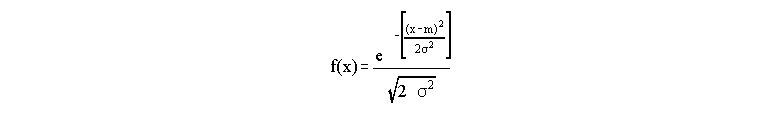
Don't worry about this equation! What is important to note is that the function is characterized by two parameters: the mean m, which tells us where the peak of the curve falls along the x axis, and the standard deviation (greek letter sigma), which tells us how wide the curve is.
So what does statistical theory tell us about being able to calculate the "correct" or expected value of a measurement? The method is different depending on whether we take a very large number of measurements, or just a few. It is often, if not usual, that when making scientific measurements, we only make a few measurements, so we will not get exactly the Normal distribution which would allow us to very precisely determine a measured value. Given a small number N of measurements, we would like to estimate the mean ("correct" value) and standard deviation (the spread of values we expect to get when making successive measurements of the same quantity). The estimate of the mean, designated M, is given by a familiar procedure:
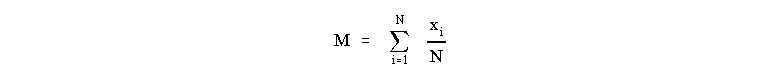
where the xi represent the experimental values. (Recall, these symbols mean "sum up each of your measurements divided by the total number of measurements.")
Similarly, we can only estimate the standard deviation, S:
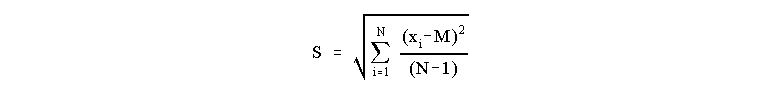
(Notice that it is not possible to get an estimate of the standard deviation by making only a single measurement.) This last computation looks complicated but, in practice, is simple to perform. For example, suppose we use a meter stick to measure the length of some object. A table of our results might look as follows:
| measurement | result | (xi - M) | (xi - M)2 |
| x1 | 10.13 cm | - 0.10 | 0.0100 |
| x2 | 10.24 | + 0.01 | 0.0001 |
| x3 | 10.09 | - 0.14 | 0.0196 |
| x4 | 10.41 | + 0.18 | 0.0324 |
| x5 | 10.26 | + 0.03 | 0.0009 |
| SUM | 51.13 | 0.0630 |
Thus,

| Concept Check: Notice that since we do not have an expected
"correct" answer here, we cannot know whether there is systematic
error assuming we trust our measuring instruments. If the measuring
instruments are calibrated/trusted, then the fluctuations of each
individual answer in the table are most likely due to random error, with
the "correct" answer being somewhere close to this M, and each
individual answer fluctuating around the mean by approximately S. With the coin-flips concept-check, above, assuming the coins are evenly weighted, differences from the expected value of 5 would be due to random fluctuations. You would expect to get 3 heads as many times as 7 heads if you flipped them many times. But, it is possible to have both systematic and random error (you can never eliminate random error) if, for example, some of the coins are weighted so that you should expect one outcome more than the other. So the real mean (after many flips) may be 6 instead of 5, and you will still get random fluctuations about that mean. |
In most cases, we will actually use a computer to calculate M and S, but we do need to know where they come from. Now we ask the question: "What is the probability that my estimate of the mean, M, based upon a small number of measurements, will fall close to the true mean, m, which is based on a large (ideally, infinite) number of measurements?" What we want to estimate here is not the standard deviation (spread) of the measurements, but the standard deviation (spread) of means (estimated "correct" values) - if we know how much the mean values are expected to be spread out, then we know the correct value is likely to be in that spread. The estimated spread of the mean measured values is called the standard error, abbreviated SE.
Theory tells us that a good estimate of the standard deviation in measured mean values, SE, is
![]()
Notice that although our estimate of the mean, M, and standard deviation, S, might not change appreciably as the number of measurements, N, is increased, the standard error, SE, gets smaller with larger N. It is important to know that this estimate of the standard error is an approximation that is only valid for small N and does not mean that the standard error goes to zero as N gets large. You should also realize that the ultimate limit on the smallness of the standard error is determined by instrumental sensitivity.
| Concept Check: In the numerical example above, the standard error is 0.13/(sqrt(5)) = 0.06 cm, and this tells us about how far the estimated mean, M = 10.23 cm, is expected to be from the "correct" value. We will see next what "how far" means. |
Again, statistical theory tells us what the standard error means to us. The standard error can be used to express our confidence in our estimate of the mean ("correct" value) as follows:
If we add or subtract the standard error to the mean, we will get a possible range of values. This is usually written as the interval M + SE. Statistics tells us that if we are only making a small number of measurements, we should expect the likelihood that the true mean (the "correct" value) is in that interval is 60%. The interval determined by M + SE is called a "60% confidence interval". In our example, we are 60% confident that the value 10.23 + 0.06 will overlap the true value.
For us, 60% is not going to be good enough. So we can make our interval bigger, making it more likely that the correct value is in there! If we add or subtract TWO standard errors to the mean, M + 2SE, for small numbers of measurements, we should expect the "correct" value to be in that interval 90% of the time, or with a confidence of 90%. In our example, we are 90% confident that the value 10.23 + 0.12 will overlap the true mean.
For some measurements, we have expected correct values (flipping 10 coins, we expect the average number of heads to be 5), and for others we do not (if we are measuring the width of a table). If we do have an expected correct value, and if your 90% confidence interval for the measured quantity does not agree with the accepted value, then you should investigate the systematic errors that may have been present in your experiment. Note that it is possible, though, that there are no systematic errors, and that statistics says that we can be only 10% confident that is the case.
Once you figure out your 90% confidence interval, such as above: 10.23 + 0.12, we can think about significant digits.
The error tells us about how unsure we are of each digit. In the above example, we are unsure of the 0.1's place to +0.1 and of the 0.01's place to +0.02. If we are already unsure of the 0.1's place, we are certainly not concerned with an additional uncertainty in a less significant digit such as the 0.01's place. The biggest uncertainty is in the largest decimal place, so the rest of the error is extraneous: you should always round errors to one significant digit. So we would have 10.23 + 0.1.
But now, we are saying we are unsure of the 0.1's place, having a measurement in the 0.01's place is meaningless, so we need to round the answer to the same decimal place as the error. So the correct answer is 10.2 + 0.1.
| Concept Check: 949 + 111 should be rounded to 900 + 100. 952 + 111 is potentially more troublesome, but just apply the rules: it should be 1000 + 100. |
