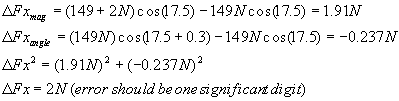Analysis
A. Graphical
You want to find the sum of your three vectors graphically. Recall this means
that we need to draw them to scale, head to tail. Do this very carefully on another
piece of paper with a ruler and protractor.
B. Analytical
In part A, you should have determined the angles of each force vector. You have read the
forces from the scales. These are your experimental numbers. Each of these
numbers has an error associated with it which is inherent in the measuring instrument: how
well can you read the measuring instrument? Before we talk about the error analysis,
lets recall how to add vectors analytically using vector components.
Using the forces read from the scales and the angles measured from your original
drawing, you can calculate the x and y components of each of your vectors. You will
then add up the x-components and y-components to get the sum - the x and y-components of
your resultant vector. From these components you can determine the magnitude and
direction of your resultant vector.
- But then we have to ask whether this is equal to what you expect the answer should be
within experimental error: to do this you must determine what you think the error is on
each force and each angle measurement. This error is due to how precisely you think
you can read the markings - this is something you determine. For example, on a
wooden meter stick with markings down to 1 mm, I doubt I can read a number to better than
0.3 mm (in my mind I can break up the divisions into 3), so 0.3 mm would be the error I
have to associate with any single measurement I make with that meter stick. What do
you estimate your error on reading the force scale and reading the protractor is?
- You now need to propagate those error measurements through your calculations in the way
we learned last week so that you end up with the components of the resultant vectors with
their associated errors. See below for an example of the error calculation on one
component, and then do this for all your components.
- When you sum the three individual components, you are again going to have to propagate
the errors from each of the three components to get the error on that component for the
resultant vector.
- You can leave your analytical result for the sum in component form with the errors.
Does it equal the expected value? Use the components to find the magnitude
and direction of the resultant vector - you need not use error analysis here - how does
this compare to what you found graphically?
Write-Up Example
I have measured a force of 149 N. I determine that the from the scale I can only
read it to within +/- 2 N. Therefore the magnitude of the force is 149 +/-2 N.
The angle I measure is 17.5 degrees from the -x axis. With the protractor, I
figure I can discern 0.3 degrees, therefore the angle is 17.5 +/-0.3 degrees.
My x-component is then Fx = (149 +/-2 N)cos(17.5+/-0.3). Without error, this
gives Fx = 142 N. What is the error in Fx (called DFx)?
Recall that it is the square-root of the sum of the squares of the error due
to only the magnitude and then only the angle:
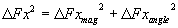
The error due to the magnitude and angle are calculated without calculus
(Physics 105) as such:
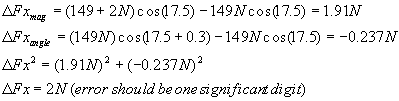
With calculus (Physics 1115), you would take the partial derivatives, instead.
***Note that when you take the derivative of a sin function, you need to use
angles in radians.***
Therefore, my answer is Fx = 142 +/-2 N.
Write-Up
-
If this is a formal lab (as indicated on the lab syllabus), you have been
instructed as to whether this is an individual or group write-up, or an oral
presentation. If it is a write-up, each person
must submit the lab electronically as a word-processed document in Moodle
before the next lab meeting. If it is a group write-up, you should all
be submitting the same document. For written formal labs, remember to check the "write-up hints" page to be sure
everything is included and check your write-up against the grading rubric.
- If this is an informal lab, work on the results together in your groups,
and be sure to have your complete informal lab in your lab notebook and
checked by the instructor before
you leave.
- Remember to read the next lab and do the pre-lab before you come to lab
next week! You may work on the pre-lab with others, but each person must
submit her or his own work.
Department
of Physics

![]()