

Introduction:
In this lab, we will review the laws of kinematics as they apply to projectile motion.
Recall that kinematics gives us the relationship between distance and time for an object undergoing constant acceleration. So for an object in projectile motion, where the acceleration is zero in the horizontal direction, we get, for the horizontal (x) and vertical (y) directions treated separately:
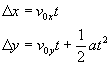
for the displacement equations.
If we shoot a projectile at an angle q up from the horizontal, then v0x = v0cos(theta).
Assuming we know all of the initial variables (velocity, angle, acceleration and beginning height above ground), we can predict the horizontal range (Dx) of the projectile by solving for time in the second equation and plugging it back into the first. This algebra can be done in a few steps, you might want to try it, but choosing UP as the positive direction, the end result is:
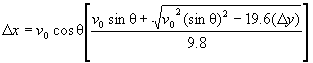 .
.
This equation can be used to determine how far our projectile is going to travel once we have determined the initial speed, initial height, and angle. Think about how, given a certain error in the speed, you can figure out the error in range.
