Physics 106 - Capacitors

OBJECTIVES

·       To define capacitance

·       To determine how the capacitance of conducting parallel plates is related to the separation distance between the plates and the surface area of the plates

·       To determine the permitivvity constant

INTRODUCTION

Capacitors are widely used in a variety of electric circuits to provide extra energy or help keep energy levels at a constant value.  As an example, a home cooling (AC) unit will have a capacitor that stores charge (energy).  When the system is started, the capacitor can release the stored energy to assist the unit in starting the compressor necessary to cool the home.  Electronics with flashing lights use a capacitor in a timing or RC circuit.

The classical design of a capacitor, which you will use in this lab, is two parallel conducting plates, separated by an insulator as shown below.

Charges of opposite sign are stored on the two plates, establishing an electric field between the plates.  The capacitance can be defined as a ratio of charge to voltage, or

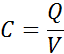
where C is the capacitance, in Farads, Q the charge on one plate in Coulombs (each plate has equal magnitude charge), and V is the separation Voltage.

However, it is a misnomer to think that the capacitance of a capacitor is defined by the amount of charge and voltage.  Capacitance is defined by the geometry of the capacitor design, or particularly on the cross sectional area of the plates and the separation distance of the plates (and also the material, if any, placed between the plates).

In this lab, you will use a pHet simulation to derive the relationship for capacitance, as a function of both separation distance and the area of the plates.

PROCEDURE

Use Capacitors Phet for this lab.

PART 1

In this part of the lab, you will determine the relationship between capacitance and plate area.  Using the simulation, fix the voltage at 1.5 V (the default), the plate Area at 100 mm² (default), and the separation distance at 5.0 mm.  Select the Capacitance meter, and measure the capacitance.  Repeat for the five values of plate area shown below.

Graph your data in EXCEL, Google Sheets, or on a graphing calculator. 

1.                  What is the mathematical function suggested by the graph (linear, quadratic/parabola, inverse/rational)?  If you are unclear as to the shapes of these graphs, visit Types of Graphs

2.                  Write a corresponding equation based on your answer, using C as the symbol for Capacitance, A as the symbol for plate Area, and k as some arbitrary constant.  For example, if you felt the relationship was linear, you would write C = kA .  If you felt the relationship was quadratic, you would write C = kA² .  If you felt this is an inverse relationship, you would write C=k/A .

PART 2

Now the relationship between Capacitance and plate separation will be investigated.  Keep the plate area at 400 mm² and the battery voltage at 1.5 V.  Complete the table below for the indicated plate separations

Graph your data in EXCEL, Google Sheets, or on a graphing calculator. 

1.                  What is the mathematical function suggested by the graph (linear, quadratic/parabola, inverse/rational)?

2.                  Write a corresponding equation based on your answer, using C as the symbol for Capacitance, d as the symbol for plate separation, and k as some arbitrary constant.  For example, if you felt the relationship was linear, you would write C = kd and so forth.

CONCLUSIONS

1. Write an equation for Capacitance (C) as a function of Area (A), separation distance (d), and a constant (k) by combining your two equations.  For example, if you felt that both relationships were linear ( C = kA and C = kd) , then you would write an equation for capacitance that shows capacitance varying linearly with both A and d, or C = kAd .  Write a brief statement justifying your decision.
2.  Find the equation for Capacitance as a function of Area and distance from a reputable source (text, appropriate website), and copy the equation and source below.  If your equation above does not match, explain why your equation in #1 was incorrect. 
3. You now know that the constant k we used throughout the lab is the permittivity of free space, $\epsilon_0$.  Research what this constant represents and report your findings below
4. Choose any one set of data from either table (a known value of C, A, and d) and calculate $\epsilon_0$.    Show your work.
5.   If your value in 4 differs from the actual value (8.85 x 10¹²), explain why you think this difference exists.

Write-Up

1. If this is a written formal lab (as indicated on the lab syllabus/calendar), you will have until the next lab to submit the write up to the appropriate assignment in Moodle. For written formal labs, remember to check the "write-up hints" page to be sure everything is included and check your write-up against the grading rubric.
2. If this is an informal lab, record your results in your lab notebook. Before the next lab you will need to complete the informal lab quiz in Moodle in which you will type in your results and/or answer some questions about the lab.
3. If this is an oral report lab, you will schedule a time to meet with your instructor over Zoom to present your work. You should prepare your results and the answers to any questions in a neat and organized fashion so that you can refer to when necessary during your discussion.
4. Remember to read the next lab and do the pre-lab before the next scheduled lab session. You may work on the pre-lab with others, but each person must submit her or his own work.