PHYSICS 116

Properties of Waves and Sound

Text Reference:  Haliday, Resnick, Walker 16.4-16.6, 16.12-16.13, 17.2-17.3

Introduction

When a wave of sinusoidal shape travels through a medium, the relationship between speed v, frequency f and wavelength l is given by the simple equation

(1)

Waves having more complicated shapes may be built up by the superposition of simple sinusoidal waves of different frequencies and wavelengths.

In this laboratory you will study the behavior of waves on a vibrating string and sound waves in air by producing standing waves in both media.  Standing waves are produced when you oscillate a medium of fixed length (e.g. a fixed length of string as on a guitar) at just the right frequency.  The waves travel down the string and bounce back, adding together in just the right way to get the standing wave.  You can see more information on standing waves here.

Materials

• Computer
• Free CK12 account (www.ck12.org)

Procedure: Doppler Effect

1)      Go to http://interactives.ck12.org/simulations/physics/doppler-ducks/app/index.html?referrer=ck12Launcher&backUrl=http://interactives.ck12.org/simulations/

2)      Use the sliders to set the wave speed to 4 m/s and fill in the table below describing the relative movement of the duck and boat and the shift in frequency.

3)      The general form of the Doppler effect equation is

 f

where f’ is the observed frequency, v_D is the speed of the detector, v_s is the speed of the source, v is the speed of the wave and f is the emitted frequency. Plus or minus is determined by whether the motion will increase of decrease the observed frequency.  Calculate the expected observed frequency when the duck velocity is 1 m/s, the boat velocity is -2 m/s, the wave speed is 4 m/s and the emitted frequency is 2.0 Hz.

4)      Use the sliders to set these conditions and check your answer.

5)      Use the simulation to develop and conduct an experiment to determine if observed wave speed is affected by the Doppler effect.

6)      Set the magnitude of the duck velocity greater than the wave speed and record what happens (be sure to play the simulation).

Procedure: Longitudinal Waves in Air

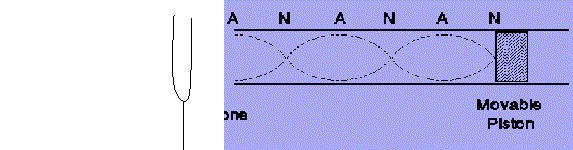
Musical wind instruments (flute, saxaphone, etc) use standing waves in air columns to produce their sounds.  Standing waves in an air column are just like standing waves on a string, except that the wave is a density wave, and you cannot see them. The simplest wind instrument is simply an empty tube: have you ever blown into the open end of a drink bottle to produce a tone? This process is used in a pan flute and other musical instruments. The length of the empty tube corresponds to specific wavelengths for standing waves and (along with the speed of sound) frequencies. The frequencies that we hear are ones that produce an antinode at the mouth of the pipe (shown with an A in the figure below). We will create standing waves in the tube in order to determine the speed of sound in air.

1)      Go to http://interactives.ck12.org/simulations/physics/pan-flute/app/index.html . Watch the introductory information or use the arrow to the right to skip.

2)      The graphs on the page show the amplitude of particle movement in the tube (upper left) and the harmonic frequencies (upper right). You can click on the white circles to read the values from the graphs. Use the information from the graphs to determine the speed of sound with a 90% confidence interval. If you need help, watch the tutorial for further explanation. Remember that the speed of a wave (like sound) is the product of the wavelength and frequency. When you click on a white dot on the graph in the upper right (record the frequency), the graph on the upper left adjusts to show the particle movement associated with the frequency. Can you use the upper left graph to determine wavelength? The speed of sound in air at 20° C is 343 m/s. How does your answer compare?

3)      Determine how the fundamental frequency (the 1^st harmonic) relates to the other harmonic frequencies. Develop an equation that relates the n^th harmonic to the fundamental frequency.

Write-Up

1. If this is a formal lab (as indicated on the lab syllabus), you have been instructed as to whether this is an individual or group write-up, or an oral presentation. If it is a write-up, each person must submit the lab electronically as a word-processed document in Moodle before the next lab meeting. If it is a group write-up, you should all be submitting the same document. For written formal labs, remember to check the "write-up hints" page to be sure everything is included and check your write-up against the grading rubric.
2. If this is an informal lab, work on the results together in your groups, and be sure to have your complete informal lab in your lab notebook and checked by the instructor before you leave.
3. Remember to read the next lab and do the pre-lab before you come to lab next week! You may work on the pre-lab with others, but each person must submit her or his own work.

Department of Physics