Kater’s Reversible Pendulum

Purpose: To measure the acceleration due to gravity in Lynchburg as precisely and accurately as possible. We would like to determine it to a scientific precision of 1 part in 104~105, or
filler image.

Note: If you are looking to purchase a high quality Kater's Pendulum (reversible pendulum, physical pendulum), contact Professor Peter Sheldon at Randolph College (psheldon@randolphcollege.edu) - I can help you get one a lot cheaper than the few I have found in the standard catalogs!

Apparatus:

Background:  

Do some research to determine why we might want to determine g so carefully - perhaps g is pertinent in some other experiments?  Try to find a published, precise value of g for the local area.  What is g dependent on locally?  Hint: g is primarily dependent on lattitude; can you find a reference which gives you that relationship?  What should g be for our lattitude?

filler image

Theory:

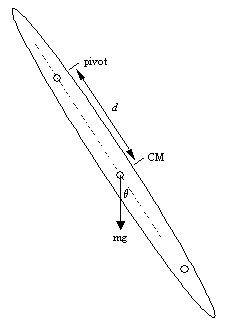
Using Newton's Second Law in a standard way, we have seen that we can determine that a physical pendulum (mass, m, moment of inertia, I, and distance from pivot to CM, d1) undergoes simple harmonic motion, and has a period

(1) T = 2p (I/mg d1)1/2

Where are approximations made in the derivation of this period for a pendulum? We assume damping is small, (Is it? We should estimate beta. See analysis.) And q is small, (How small is small? See analysis.)

By the parallel axis theorem,

(2) I = Icm + md12, so

(3a) T1 = 2p ((Icm + md12)/mg d1)1/2

If we instead suspend the pendulum from a different position (other end - this is the "reversible" nature of this pendulum),

(3b) T2 = 2p ((Icm + md22)/mg d2)1/2.

If we can adjust the distribution of the mass so that the periods are equal when hung from either end, then what is the period?

When periods are equal, T = T1 = T2, and

(4) ((Icm + md12)/mg d1)1/2 = ((Icm + md22)/mg d2)1/2

and this simplifies to

(5) Icm = m d1 d2, 

and plugging back into (3a or 3b),

(6) T = 2p ((d1 + d2)/g)1/2.

Let's define L = (d1 + d2) as the length between the two pivot points (knife edges). Then if we can measure T, the period when the periods are equal from both pivots, and L precisely, we have a precise measurement of g:

(7) g = 4p2L/T2.

Procedure:

How can we determine equal period T precisely?

The pendulum has knife-edges at either end from which it can be hung to oscillate. Outside of these two knife-edges are moveable masses. If we fix one mass (A) at a distance, relatively close works fine, from a knife-edge, and then measure the period hung either way up for various positions of the other mass (B), we can then determine which position of B allows for equal periods when hung either way up.

  1. Level the platform that the pendulum swings from. (This is not absolutely crucial—we try reasonably well.)
  2. Avoid corrosion on platform—use a light coating of oil on the platform surface.
  3. Place the movable bobs (masses) outside of the knife edges like this:

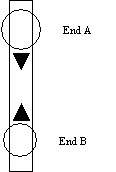
    4. filler image

  4. We are only going to move B, so we only need to know its position. Measure the positions of the bob from the "top" (dull end) of the knife edge to the nearest rim of the bob. This allows us to locate the bob using calipers with 0.01 cm precision.
  5. Move the small bob somewhere near the middle of the length of pendulum that it is on, and measure the distance from the knife edge. The image below gives an example (the actual distance of 9 cm is not meaningful)

    filler image

  6. Carefully and gently place end A knife edge on the platform. Care is required because the knife edges are hardened and the platform is not, so the platform can be dented by the knife edges or the knife edges chipped.
  7. Swing the pendulum. Remember, the amplitude should be small. Let the pendulum swing for 30 sec or so to allow it to settle down. measure the period.
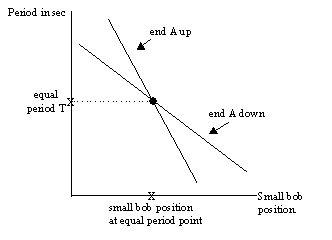
  8. Several determinations of the period are now made—first with end A up (as in steps 6-7), and then with end A down.  The small bob is moved and the period measurements are repeated in an attempt to fined the positions where the period with end A up equals the period with end A down. You might consider initially moving the bob a few cm each time. Once you have approximately located the equal period position (step 10), you might go back and take some more data near that position.

    To determine the period for each position of the bob, you will need to make measurements for multiple periods in order to decrease the error (see Note 1 below). A photogate does not have human reaction time (as opposed to you with a stopwatch), so devise a way to use a photogate.

  9. A graph of period vs. small bob position is made and two lines are plotted. One line represents the variation of period with bob position when end A is up. The other line represents the variation of period with bob position when end A is down. The place where the two lines intersect gives us the value of the equal period:

    10. filler image

    Near the equal period point straight lines fit the data very well. Note that using this method, you never have to actually take data at the equal period point!

  10. Determine the length L between the knife edges.  Currently, this is probably the largest source of error in this experiment. The best we can do is carefully use a meter stick.  How precise a measurement can you make with a meter stick?  If you come up with a better way of measuring, by all means, do so.
  11. Calculate your value of g with error:

    From Equation (11) we determine g = 4p2L/T2, with error as follows

    filler image

    Note that if we want the fractional error in g to be

    filler image

    then, the fractional error is L and in T should be about that much also.

Additional Analysis

  1. Be sure to compare g to your expected value accounting for lattitude.
  2. This is an example of a precision measurement.  Precision measurements are very painful to make because you have to try to take into every possible source of error.  What are ALL the possible sources here? You want to come up with an exhaustive list.  What about the accuracy of the computer's clock.  I suggest you check the approximate accuracy to make sure that the error added by the clock is negligible to the other errors involved.  A simple way to do this is to compare the timing done in LoggerPro to the best time standard we have - the atomic clock.  You can observe the atomic clock here.  Perhaps start LoggerPro timing one evening, and write down the exact atomic clock time when you start it going; come in the next morning and stop it timing, while watching the atomic clock.  Compare the time elapsed for the two clocks.
  3. Damping would affect the predicted period of the pendulum.  Reference the next experiment (Lab 3 Harmonic Oscillator), Equations 2.3 and 2.5. Note that equation 2.3 is just our solution to the equation of motion, but it has the addition of an exponential damping term. Determine an approximate value for beta to see if it would affect the period to more than 1 part in 105. You can determine an approximate value for the damping by taking just three or four amplitude measurements far apart in time.  Set the pendulum going and measure the amplitude.  Come back some time later (1 hour?), and measure the amplitude again and the time elapsed, repeat.  From those measurements, you can determine an approximate value for beta.
  4. What does q being small mean?  At what value of q is the angle within 1 part in 105 of sinq?  Exhibit this with a graph of the percent error between theta (the approximation) and sinq (the exact value) versus q.  You can do this easily in Mathematica, Matlab, Excel, or any other program you like.  Remember, q is in radians.
  5. Address in your conclusions why this might be a better way of determining g than using any other pendulum: a simple pendulum or a non-reversible physical pendulum.

Experimental Notes

Note 1: Precise determination of the period for a given position of the masses is essential. If we wish to precisely determine g to 5 significant figures we must determine T that well also (see Procedure step 12):

filler image.

The End