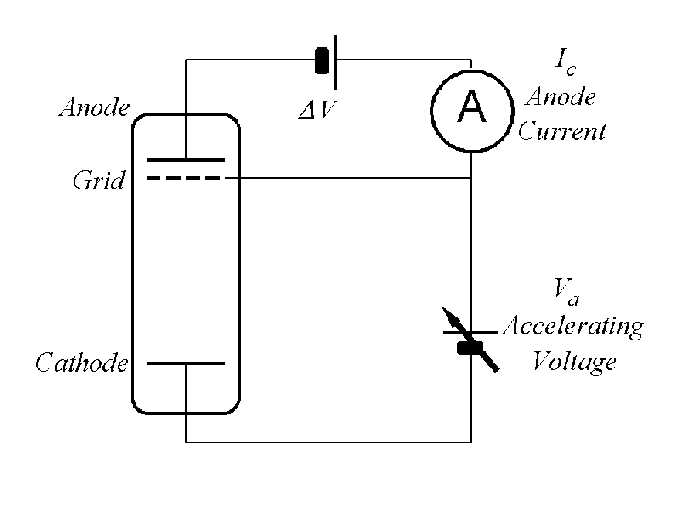
Simplified Circuit for Franck-Hertz Experiment
PHYSICS 322 LAB
THE FRANCK-HERTZ EXPERIMENT
OBJECT:
To demonstrate, through the study of collisions between electrons and gas molecules, that the energy is indeed quantized in atomic interactions.
APPARATUS:
A mercury-filled Franck-Hertz tube, an electric oven, a control unit providing various power supplies and a DC current amplifier, and oscilloscope.
BACKGROUND:

Simplified Circuit for Franck-Hertz Experiment
In an oven-heated vacuum tube containing mercury
gas, electrons are emitted by a heated cathode, and then accelerated toward a grid that is
at a potential, Va, relative to the cathode. The anode (plate) is at a lower
potential, Vp = Va - DV. If electrons havesufficient energy when they reach the
grid, some will pass through and reach the anode. They will be measured as current Ic
by the ammeter. If the electrons do not have sufficient energy when they reach the grid,
they will be slowed by DV, and will fall back to the grid.As long as the
electron/molecule collisions are elastic, the collector current depends only on Va
and DV
since the electrons lose no energy. However, Franck and Hertz discovered that Ic
went through a series of maxima and minima as Va was varied. This implies that
the gas molecules absorb energy from the electrons only at specific electron energies
(resonant energies).
For example, the first excited state of mercury
is 4.9 eV above the ground state. This is thus the minimum energy that mercury atoms can
absorb from the accelerated electrons. Hence, if Va< 4.9 volts, any
collisions are elastic and if Va >DV, many electrons pass through the grid and reach the
anode, to be measured as Ic. If Va= 4.9 volts, the electrons gain
enough kinetic energy to collide inelastically with the mercury atoms just when they reach
the grid. In these interactions, the mercury atoms absorb 4.9 eV. Thus, the electrons lose
the same amount and no longer have sufficient energy to overcome DV. They fall back to the grid
and Ic is a minimum. As Va is raised beyond 4.9 volts, Ic
increases again. However, when Va reaches 9.8 volts, the electrons can lose all
their energy in two collisions with mercury atoms in two inelastic collisions between the
cathode and grid. Again, these are pushed back onto the grid, and Ic falls to a
minimum. Current minimum are found whenever Va is a multiple of 4.9 volts.
This simplified description neglects contact
potentials. Therefore, Va will need to be some higher than 4.9 volts when the
first minimum occurs. Nevertheless, all successive current minima should differ by
multiples of 4.9 volts from the first minimum.
THE EXPERIMENT
M = Plate or Anode
A = Grid (not Anode!)
H = Filament Heater
K = Cathode
Ub = Accelerating voltage Va
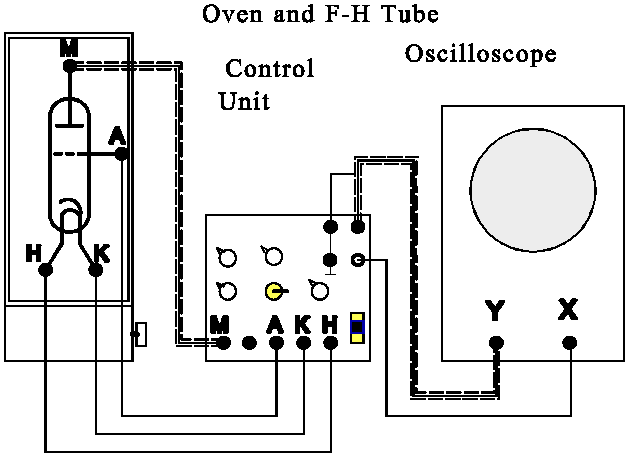
Heater = midrange (about 5.5 volts)
Gain-Amplifier = midrange
Zero-Amplifier = midrange
Adjust Va = zero
Switch Va = ramp (a sawtooth waveform
voltage)
Oscilloscope X-Channel = about 0.5 volts/cm
Y-Channel = about 0.5 volts/cm
ANALYSIS
Note that on the oscilloscope trace the vertical
deflection is proportional to the anode current Ic, and the input to the
x-channel of the oscilloscope is equal to Va/10.
From the oscilloscope trace, measure volues of Va
for which the collector current (Ic) is a minimum. Then tabulate the voltage
difference between adjacent minima.
You should find that the current minima are
spaced at intervals of 4.9 volts, showing that the excitation energy of the mercury atom
is is 4.9 eV.
The spectral frequency corresponding to this energy is 1.18 x 10-15 Hz.
The corresponding wavelength is 253.7 nm.
In their original experiments, Franck and Hertz
verified the prescence of the ultraviolet radiation with the aid of a quartz spectrometer.