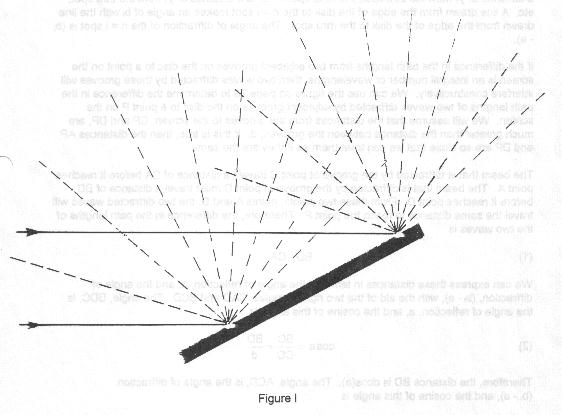
The surface of a compact disc is covered with concentric grooves, and when a laser beam shines on it most of the light is reflected. However, the light that strikes the grooves is scattered in all directions, as illustrated in Figure 1. 

The light scattered from two of the grooves interferes constructively at only certain locations, which results in a diffraction pattern. The origin of this diffraction pattern is similar in concept to that produced from two slits. The locations of the regions of constructive interference can be determined by considering the difference in the path lengths between two beams of light that strike adjacent grooves on the disc.

Figure 2 provides an illustration of the experimental parameters. 

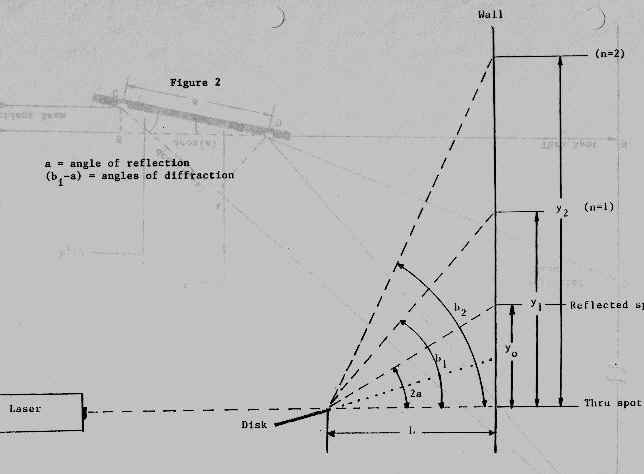
The beam from a He/Ne laser strikes a compact disc that is tilted at a slight angle (a) from the horizontal. A screen is placed a distance (L) beyond the disc. The disc is situated so that the beam strikes its edge in such a way that some of the beam passes straight on to the screen creating a "thru spot". Most of the light that strikes the disc is reflected by an angle of (a) from the plane of the disc (the angle of reflection is the same as the angle at which the incident beam strikes the disc), resulting in a reflected spot on the screen. The reflected spot is a distance of y_o from the thru spot. If we draw lines from the edge of the disc to the reflected spot and the thru spot, then the angle defined by these lines is 2a. A series of additional spots appear on the screen above the reflected spot. These spots are the result of constructive interference between waves diffracted by adjacent grooves on the disc. The first spot (n=1) is a distance of y₁ from the thru spot, the next spot (n=2) is a distance of y₂ from the thru spot, etc. A line drawn from the edge of the disk to the n = i spot makes an angle of b_i with the line drawn from the edge of the disk to the thru spot. The angle of diffraction of the n = i spot is (b_i - a).

This is the same analysis which was done for two slit interference, so you can probably skip to the experiment. If the difference in the path lengths from two adjacent grooves on the disc to a point on the screen is an integral number of wavelengths, then two waves diffracted by those grooves will interfere constructively. We determine the difference in the path lengths of two waves diffracted by adjacent grooves on the disc to a point P on the screen using Figure 3. We will assume that the distances from the grooves to the screen, CP and DP, are much greater than the distance between the grooves, d. If this is true, then the distances AP and DP are so close that we can treat them as if they are the same.

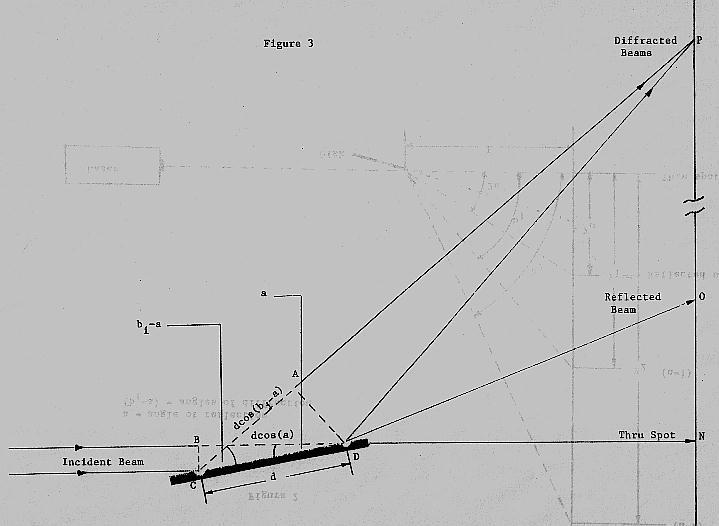
The beam that is diffracted by the groove at point C travels a distance of CA before it reaches point A. The beam that is diffracted by the groove at point D must travel a distance of BD before it reaches point D. From these two points, points A and D, the two diffracted waves will travel the same distance to reach the point P. Therefore, the difference in the path lengths of the two waves is

(1)

We can express these distances in terms of the angle of reflection, a, and the angle of diffraction, (b_I - a), with the aid of the two right triangles, CAD and BCD. The angle, BDC, is the angle of reflection, a, and the cosine of this angle is

(2)

Therefore, the distance BD is dcos(a). The angle, ACD, is the angle of diffraction,

(b_i - a), and the cosine of this angle is

(3)

Therefore, the distance CA is the same as dcos(b_i - a). The substitution of these expressions into equation 1, yields the condition for constructive interference:

(4)

where i is an integer.

We can use this equation to determine the distance between the grooves on the disc, but to do so requires the knowledge of the angles of reflection and diffraction. These can be calculated with the aid of Figure 4.

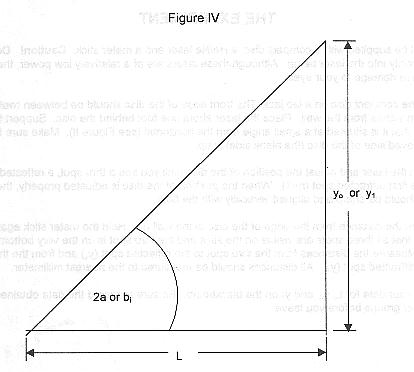
The tangent of the angle, 2a, is

(5)

We can obtain an equation for the angle b_i with a similar analysis.

(6)

The problem of determining the distance between adjacent grooves now reduces to one of measuring a few distances. The experimental procedure follows.

• Laser
• Meter stick
• CD (there are plenty on the optics shelves in the equipment room)

Place the compact disc on a surface so that you can shine the laser directly at it. The front edge of the disc should be between twelve and fourteen inches from the wall. Place the laser about one foot behind the disc. Support the disc so that it is situated at a small angle from the horizontal (see Figure 2). Make sure that the grooved side of the disc (the side with no writing) is up.

Turn on the laser and adjust the position of the disc until you see a thru spot, a reflected spot, and the first diffracted spot (n=1). When the position of the disc is adjusted properly, the three spots should be sharp and aligned vertically with the floor.

Measure the distance from the edge of the disc to the wall (L). Hold the meter stick against the wall so that all three spots are visible on the stick and the thru spot is on the very bottom of the stick. Measure the distances from the thru spot to the reflected spot (y_o) and from the thru spot to the diffracted spot (y₁). All distances should be measured to the nearest millimeter.

Calculate the distance between the grooves (d) from Equation 4 after determining the angles a and b₁. The wavelength of the laser (l ) is 632.8nm and i = 1. Calculate the number of grooves per millimeter on a compact disc (d^-1) with error.

Laser Lab Home    Speed of Light    Diffraction    CD-Diffraction